您當前位置:首頁 > 知產百科 > 文章正文
年金終值與年金現值公式的解讀(終值和現值例題)
年金終值與年金現值公式的解讀
一、年金:指 等額、定期的系列收支。例如分期付款賒購、分期償還貸款、發放養老金等。
二、普通年金 /后付年金:從第 1 期開始,每期期末收付的等額款項
1.普通年金終值:每期期末等額收付款的復利終值之和。
終值F=A*((1+i)n-1)/i=A*(F /A,i,n)
償債基金:為使年金終值達到既定金額每期期末應收付的金額。
A=F/(F /A,i,n)
償債基金系數與普通年金終值系數互為倒數
2.普通年金現值:每期期末等額收付款的復利現值之和。
現值P=A*(1-(1+i)-n)/i=A*(P/A,i,n)
投資回收額:為使年金現值達到既定金額每期期末應該收付的數額
A=P/(P/A,i,n)
投資回收系數與普通年金現值系數互為倒數
三、預付年金:從第 1 期開始,每期期初收付的等額款項。
終值F=A*(F /A,i,n)*(1+i),現值P=A*(P/A,i,n)*(1+i)
四、遞延年金:即 從第 2 期或第 2 期以后開始,每期發生等額的款項
終值F=A*(F /A,i,n),
現值P
(1)復利現值求和法。即 分別計算各個等額款項的復利現值之和。
(2)兩次折現法。即 把 n 期等額款項按照年金現值計算法,求出遞延期末的現值,然后再將此現值調整到第一期期初。
3.扣除法。 假設遞延期內也有等額款項發生,先計算(m+n)期年金現值,然后扣除遞延期間并未發生的等額款項的年金現值。
五、永續年金:無限期的每期收付等額款項
無終值,現值A=P/i
【例題·單選題】企業打算在未來三年每年年初存入2000元,年利率2%,單利計息,則這三筆存款的現值是()元。
A.5927.57
B.6243.2
C.6240
D.5883.86
『正確答案』D
『答案解析』2000/(1+2*2%)+2000/(1+2%)+2000=5883.86
【例題·多選題】下列說法中,正確的有()
A.復利現值系數與復利終值系數互為倒數
B.復利現值=復利終值(1+i)
C.年金現值等于各個A的復利現值之和
D.年金終值等于各個復利終值之和
『正確答案』ACD
『答案解析』復利現值與復利終值之間并不是乘以(1+i)的關系,復利現值=復利終值/復利終值系數,選項B不正確

推薦閱讀:
最新文章
 稅務登記證可以注銷嗎(稅務注銷需要什么材料和流程)
稅務登記證可以注銷嗎(稅務注銷需要什么材料和流程)
 注冊一個公司的流程怎樣費用多少(注冊公司的手續和費用標準)
注冊一個公司的流程怎樣費用多少(注冊公司的手續和費用標準)
 辦理股東變更需要什么資料(股份變更流程)
辦理股東變更需要什么資料(股份變更流程)
 寧波注冊公司流程及費用(寧波注冊公司的完整流程)
寧波注冊公司流程及費用(寧波注冊公司的完整流程)
 辦理分公司需要帶什么資料(注冊分公司的流程和所需材料)
辦理分公司需要帶什么資料(注冊分公司的流程和所需材料)
熱門文章
如何查詢中小企業名單(中小微企業名錄查詢系統入口)5641人閱讀
 國家企業信用公示信息系統山西入口(企業信息公示年報流程)
國家企業信用公示信息系統山西入口(企業信息公示年報流程) 3914人閱讀
 如何查詢商標注冊情況(注冊商標名稱查詢詳細步驟)
如何查詢商標注冊情況(注冊商標名稱查詢詳細步驟) 2541人閱讀
 廣州紅盾網企業信息查詢系統入口(紅盾網企業信息查詢流程)
廣州紅盾網企業信息查詢系統入口(紅盾網企業信息查詢流程) 1976人閱讀
 國家企業信用公示信息系統湖北入口(工商年報公示流程)
國家企業信用公示信息系統湖北入口(工商年報公示流程) 1662人閱讀
 內蒙古企業信用信息查詢公示系統入口(企業公示年報流程)
內蒙古企業信用信息查詢公示系統入口(企業公示年報流程) 1555人閱讀
 遼寧省企業信用公示信息系統入口(工商年檢具體操作步驟)
遼寧省企業信用公示信息系統入口(工商年檢具體操作步驟) 1413人閱讀
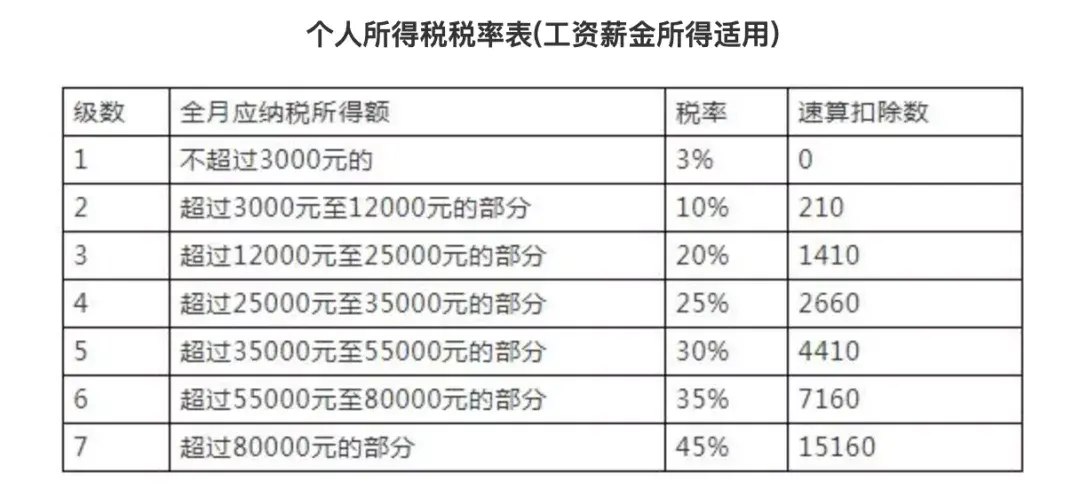
 員工工資超過5000怎么扣稅(5000以上扣稅標準稅率表)
員工工資超過5000怎么扣稅(5000以上扣稅標準稅率表) 1392人閱讀
 食品經營許可證網上申請登錄入口(山東食品經營許可備案系統操作流程)
食品經營許可證網上申請登錄入口(山東食品經營許可備案系統操作流程) 1206人閱讀
 國家企業信用公示信息系統四川入口(企業信用信息公示填報流程)
國家企業信用公示信息系統四川入口(企業信用信息公示填報流程) 1146人閱讀






.png)
.png)
.png)




